Prime numbers have fascinated mathematicians for centuries. These seemingly simple yet incredibly complex mathematical objects are the foundation of many branches of mathematics and have applications in areas ranging from cryptography to biology. In this article, we take a closer look at prime numbers, their properties, the history of their research, and their importance in the modern world.
A prime number is a natural number greater than 1 that has exactly two divisors: 1 and itself. The first few prime numbers are:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, …
It is worth noting that:
The number 1 is not greater than 1 and has only one natural divisor, so it is not a prime number.
The smallest non-one natural divisor of a natural number greater than one is a prime number.
The number 2 is the only even prime number, so all prime numbers greater than 2 are odd.
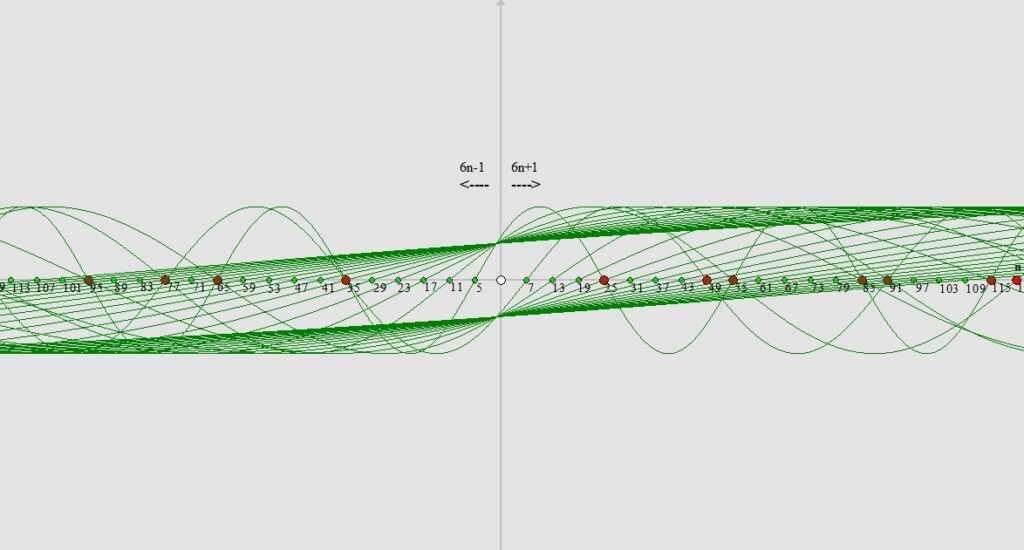
Prime numbers ≥5 (greater than or equal to 5) always have the form 6n±1 (6n-1 and 6n+1).
50% of the numbers in the Fibonacci sequence are numbers of the form 6n±1, i.e. prime and near-prime numbers.
Numbers that are the product or square of two prime numbers ≥5 (greater than or equal to 5) are near-prime numbers, they always have the form 6n±1. Subtracting from the set of numbers 6n±1 the numbers that are products and squares of numbers from the set 6n±1 we will obtain all prime numbers ≥5 (greater than or equal to 5) without any factorization.
Numbers that have more than two divisors are composite numbers, for example the number 4 already has three divisors: 1, 2, and 4.
There is no largest prime number – there are infinitely many prime numbers. Euclid, using proof by contradiction, showed that the set of prime numbers is infinite. Additionally, Euclid in his work Elements presented the first proofs that prime numbers are “fundamental components” of natural numbers, that is, that every natural number ≥4, which is not a prime number, can be factored into a product of primes. For example: 4=2×2, 6=2×3, 8=2x2x2, 9=3×3 .
The largest known prime number (as of 2023) is 2^82,589,933-1, which has 24,862,048 digits. The largest known prime number that is not a Mersenne number is: 10,223 ∙ 231172165 + 1, which was discovered in 2016 and has a decimal representation of over 9 million digits.
Classes and types of prime numbers
- Twin Numbers: Two prime numbers whose difference is 2, for example (3, 5), (11, 13). The question of whether there is an infinity of these numbers remains unresolved.
- Quadruples: Four prime numbers that are of the form (p, p+2, p+6, p+8), e.g. (5, 7, 11, 13).
- Mersenne numbers: Numbers of the form ( M(n) = 2^n – 1 ) are prime numbers. Examples are 3, 7, 31, 127. Many of the largest known primes are Mersenne numbers.
- Germain numbers: Prime numbers p for which ( 2p + 1 ) is also prime, e.g. 2, 3, 5.
Historical Moments in Prime Numbers
- 3rd century BC – Sieve of Eratosthenes, a method for finding prime numbers.
- 1640 – Pierre de Fermat formulates Fermat’s Little Theorem.
- 1859 – Bernhard Riemann publishes his paper on the distribution of prime numbers.
- 1896 – Jacques Hadamard and Charles Jean de la Vallée-Poussin independently prove the prime number theorem.
- 2018 discovery of the formula for prime numbers, discovery of near-prime numbers.
Methods of determining prime numbers
One of the most well-known methods for determining prime numbers in a given interval is the Sieve of Eratosthenes. This algorithm works like this:
- A list of natural numbers from 2 to n is created.
- The first number is marked (2) and all multiples of it are crossed out.
- These steps are repeated until the end of the list is reached.
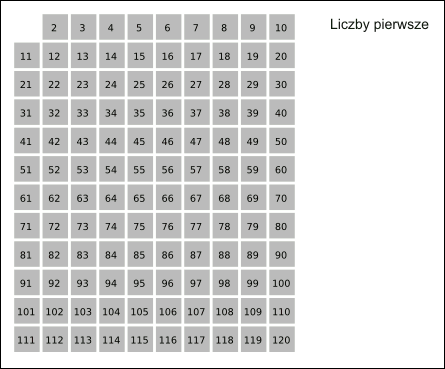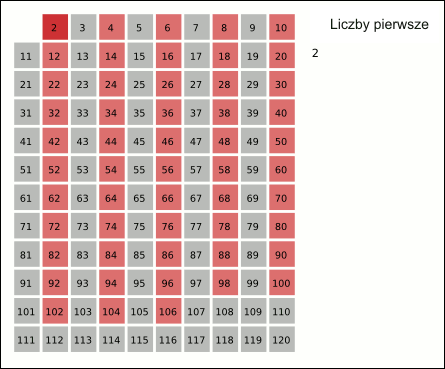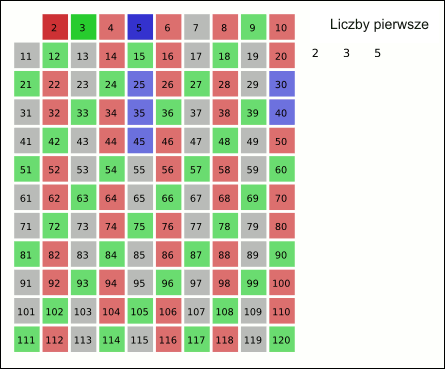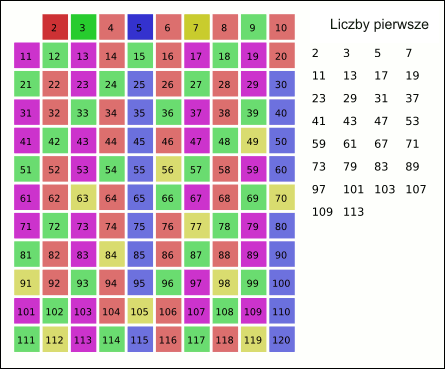
Animation_Sieb_des_Eratosthenes.gif: Saperaudderivative work: Bartek444, CC BY-SA 3.0 http://creativecommons.org/licenses/by-sa/3.0/, via Wikimedia Commons
There are many other methods for finding prime numbers. Here are a few:
- Primality test – algorithms for checking whether a given number is prime is the Solovay-Strassen primality test.
- Miller–Rabin test – a probabilistic primality test, often used in practice for very large numbers.
- AKS method – a deterministic polynomial-time primality testing algorithm.
- However, the most optimal and error-free method of finding prime numbers, without factorization, is to use the following formula:
{(2), (3), (5), (6m+1), (6n-1) | m > 0, m mod 10 ≠ 4, m mod 10 ≠ 9, n > 0, n mod 10 ≠ 1, n mod 10 ≠ 6} \ {(6m+1)*(6n-1), (6m+1)*(6m+1), (6n-1)*(6n-1) | m > 0, m mod 10 ≠ 4, m mod 10 ≠ 9, n > 0 , n mod 10 ≠ 1, n mod 10 ≠ 6}
For more information about this pattern, see the PRIME NUMBERS CODE tab.
Distribution and occurrence of prime numbers
One of the most important issues related to prime numbers is their distribution. Although prime numbers seem to appear quite irregularly, there are certain regularities in their distribution.
The prime number theorem states that the density of primes decreases logarithmically as the number of primes increases. More precisely, the number of primes not exceeding n is asymptotically equal to n/ln(n). Leonhard Euler proved that the series of reciprocals of all primes diverges. This suggests that the primes are distributed in such a way that they cannot be too sparsely distributed on the number line, which leads to the conclusion that there is an infinite number of primes. The distribution of primes on the number line is an interesting topic of mathematical study. Discoveries such as the Ulam spiral have suggested certain statistical regularities, but there is an orderly and uniform pattern to the occurrence of primes.

More information in the NEAR-PRIME NUMBERS tab.
Problems with prime numbers
Despite many years of research, there are still many unsolved problems related to prime numbers. Here are some of them:
- Riemann’s hypothesis – concerns the distribution of prime numbers and is considered one of the most important unsolved problems in mathematics. However, the occurrence of zeros of the Riemann function and the distribution of energy levels of heavy atom nuclei are strongly dependent also on near-prime numbers, and not, as is commonly believed, only on prime numbers.
- Twin primes conjecture – are there infinitely many pairs of primes that differ by 2?
- Goldbach’s Conjecture – Is every even number greater than 2 the sum of two prime numbers?
- The problem of the existence of infinitely many Mersenne primes.
- Prime numbers in the Fibonacci sequence.
- The presence of a prime number in the interval between ( n^2 ) and ( (n+1)^2 ).
Application of prime numbers
Prime numbers have many practical applications, especially in the fields of cryptography and digital security. Here are some of them:
- Asymmetric cryptography – The RSA and ElGamal systems are based on the difficulty of factoring large numbers into prime factors.
- Key Generation in Cryptography – Large prime numbers are used to generate secure keys.
- Correcting codes – Some correcting codes use properties of prime numbers.
- Pseudorandom number generators – Prime numbers are used in some pseudorandom number generation algorithms.
Prime Number Trivia
Mersenne primes are primes of the form 2^p – 1, where p is a prime number.
Fermat primes are primes of the form 2^(2^n) + 1. The first five are primes, but it is not known whether there are any others.
There are primes that remain prime after removing any number of digits from the left side – these are called left-truncated primes, e.g. 23 (3), 317 (17) (7), 3797 (797) (97) (7).
Prime numbers up to 100, 1000, 10000, 100000 and the first 10000 primes can be found here.
Prime numbers, despite their apparent simplicity, hold many secrets and are still the subject of intense mathematical research. Their properties and applications make them one of the most fascinating areas of mathematics. However, the scientific world should take a closer look at the products and squares of primes and consider the near-primes numbers just as important as primes.