Ciąg liczb Fibonacciego to jedna z najbardziej znanych i rozpoznawalnych sekwencji liczb w matematyce. Każda liczba w ciągu jest sumą dwóch poprzednich: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 i tak dalej. Ciąg ten ma wiele ciekawych zastosowań w matematyce, informatyce i innych dziedzinach, m.in. w analizie algorytmów, teorii grafów, kryptografii czy statystyce. Ciekawym aspektem ciągu Fibonacciego jest stosunek kolejnych liczb, który dąży do stałej wartości zwaną Złotym Podziałem (Złotym Odcinkiem) czy też Złotą Liczbą. Złoty Podział oznaczany jest przez grecką literę φ (phi) i wynosi około 1.618033988749895.
Ja postaram się go przedstawić z całkowicie innej perspektywy.
Najpierw załóżmy że wszystkie liczby naturalne całkowite w tym również te z ciągu Fibonacciego można uzyskać z sześciu podstawowych wzorów takich jak:
6n, 6n+1 gdzie n >= 0 oraz 6n-4, 6n-3, 6n-2, 6n-1 gdzie n > 0.
Jeśli poznaliście już Państwo moją teorie na temat jak powstają liczby pierwsze szybko zauważycie że wzory 6n+1 i 6n-1 tworzą wszystkie liczby pierwsze (oprócz liczb 2 i 3) oraz liczby przypierwsze (czyli iloczyny dwóch liczb pierwszych z wyjątkiem 2 i 3). (Więcej na temat liczb przypierwszych znajduję się w dziale KOD LICZB PIERWSZYCH).
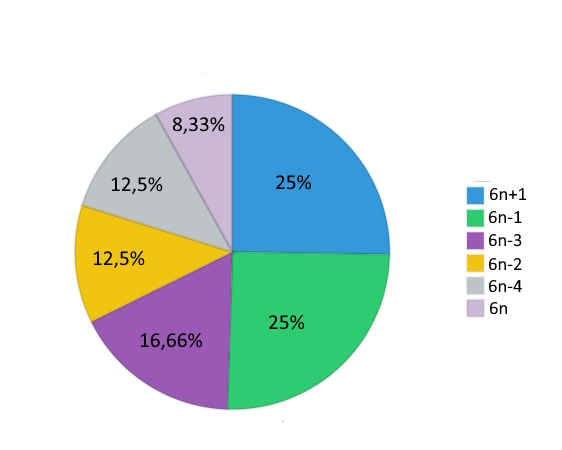
Zaskakującym faktem jest że liczby z ciągu Fibonacciego należące do wzorów 6n+1 i 6n-1 stanowią 50% wszystkich liczb znajdujących się w nieskończonym ciągu Fibonacciego.
Każda liczba z ciągu Fibonacciego o indeksie liczby pierwszej lub przypierwszej znajduje się zawsze w zbiorze liczb z omawianych dwóch wzorów 6n+1 i 6n-1.
25% liczb z ciągu Fibonacciego znajduje się w zbiorze 6n+1.
Od indeksu 1. liczby ciągu Fibonacciego (1) występują one co 6 pozycji, co stanowi 16,66%, od indeksu 2. liczby ciągu Fibonacciego (1) występują co 24 pozycje , co daje 4,16%. Co 24 pozycje od indeksu 10. liczby ciągu Fibonacciego (55) jest kolejne 4,16%.
25% liczb z ciągu Fibonacciego znajduje się w zbiorze 6n-1.
Od indeksu 5. liczby ciągu Fibonacciego (5) występują one co 6 pozycji, co stanowi 16,66%, od indeksu 14. liczby ciągu Fibonacciego (377) występują one co 24 pozycje, co daje nam 4,16%. Co 24 pozycje zaczynając od 22. pozycji indeksu ciągu Fibonacciego (17711) jest kolejne 4,16%.
12,5% liczb z ciągu Fibonacciego znajduje się w zbiorze 6n-4.
Co 24 pozycje z indeksu 3. liczby ciągu Fibonacciego (2) – 4,16%, co 24 pozycje z indeksu 6. liczby ciągu Fibonacciego (8) – 4,16%, co 24 pozycje z indeksu 21. liczby ciągu Fibonacciego (10946) – 4,16%.
12,5% liczb z ciągu Fibonacciego znajduje się w zbiorze 6n-2.
Co 24 pozycje z indeksu 9. liczby ciągu Fibonacciego (34) – 4,16%, co 24 pozycje z indeksu 15. liczby ciągu Fibonacciego (610) – 4,16%%, co 24 pozycje z indeksu 18. liczby ciągu Fibonacciego (2584) – 4,16%.
16,66% liczb z ciągu Fibonacciego znajduję się w zbiorze 6n-3.
Co 12 pozycji z indeksu 4. liczby ciągu Fibonacciego (3) – 8,33% oraz co 12 pozycji z indeksu 8. liczby ciągu Fibonacciego (21) – 8,33%.
Jednak z jakiegoś powodu ciąg Fibonacciego bardzo unika liczb ze zbioru 6n, czyli wielokrotności liczby 6.
Liczby ze zbioru 6n występują zaledwie co 12 pozycji zaczynając od 0. indeksu ciągu Fibonacciego (0), co daje nam zaledwie 8,33%.
Generalnie ciąg Fibonacciego składa się w 50% z liczb pierwszych i przypierwszych.
Jak widać na obrazku poniżej ciąg Fibonacciego tworzy 24-elementową sekwencję liczb należących do wyżej wymienionych wzorów.

Stwierdzić można że patrząc na ciąg Fibonacciego zauważamy zależność że im dalej postępuje to jest w nim mniej liczb pierwszych a coraz więcej liczb przypierwszych. Wniosek jaki się nasuwa to że właśnie liczby pierwsze i przypierwsze stanowią kluczowy punkt odniesienia w zrozumieniu wszystkich dziedzin naszego życia gdzie ciąg Fibonacciego ma zastosowanie i odwzorowanie.
Jednak w ciągu Fibonacciego powtarza się też systematycznie (od pierwszej pozycji w indeksie ciągu Fibonacciego) znowu 24-elementowa sekwencja sum cyfr każdej liczby.
Przykład; suma cyfr liczby 377 to 8 gdyż 3+7+7=17, obliczając dalej to 1+7=8.
Ciekawym spostrzeżeniem jest również fakt że suma dwóch poprzednich „sum cyfr” liczb Fibonacciego jest równa sumie cyfr kolejnej liczby Fibonacciego,
np. 13+21 czyli (1+3)+(2+1)=4+3=7
więc i suma cyfr kolejnej liczby jaką jest 34 (czyli 3+4) wynosi 7. Generalnie sprowadzamy sumę cyfr każdej liczby do wartości jednocyfrowej w zakresie od 1 do 9. Jak widzimy na rysunku poniżej.
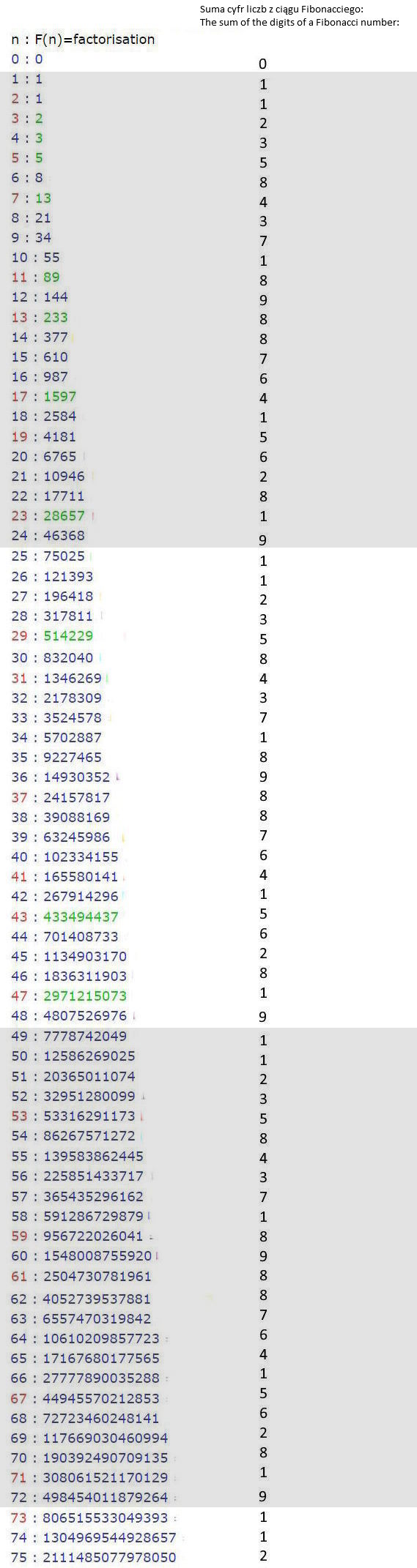
24-elementowa powtarzająca się sekwencja sum cyfr znajdujących się w ciągu Fibonacciego liczb (licząc od 1. indeksu (1)) rozkłada się według następującej kolejności: 1,1,2,3,5,8,4,3,7,1,8,9,8,8,7,6,4,1,5,6,2,8,1,9.
Liczby pierwsze w ciągu Fibonacciego (od 5 pozycji jego indeksu (5)) mają zawsze sumę cyfr wynoszącą 1, 4, 5 lub 8.
W ciągu Fibonacciego (od 5 pozycji jego indeksu (5)) brak zatem liczb pierwszych których suma cyfr wynosi 2 i 7 (gdyż liczby o sumie cyfr wynoszącej 2 i 7 występują w ciągu Fibonacciego na indeksie o wartości parzystej, a z założenia wiemy że liczby o indeksie innym niż indeks liczby pierwszej (czyli nieparzystej) w ciągu Fibonacciego nie mogą przyjąć wartości liczby pierwszej).
Dodatkowo liczbą pierwszą w ciągu Fibonacciego (od 5 pozycji jego indeksu (5)) może być tylko taka liczba której wartość sumy cyfr poprzedniej liczby wynosi 1, 3, 6, 8 lub 9. Właściwość ta jest bardzo pomocna w poszukiwaniu i faktoryzacji kolejnych liczb pierwszych w ciągu Fibonacciego.
Ponad 20,83% liczb w ciągu Fibonacciego posiada sumę cyfr wynoszącą 1.
Następne 20,83% liczb w ciągu Fibonacciego posiada sumę cyfr wynoszącą 8.
Po 8,33% otrzymują sumy cyfr: 2, 3, 4, 5, 6, 7 oraz 9.
Ciąg Fibonacciego składa się w 66,66% z liczb nieparzystych, a tylko w 33,33% z liczb parzystych.
Od indeksu trzeciej liczby w ciągu Fibonacciego co 3 pozycje są liczby parzyste.
Statystycznie w ciągu Fibonacciego występuje więcej liczb pierwszych znajdujących się w zbiorze 6n-1.
Ten artykuł jest dostępny także w języku angielskim, kliknij tutaj.