LICZBY PIERWSZE - Liczby pierwsze

Liczby pierwsze od wieków fascynują matematyków. Te pozornie proste, a jednocześnie niezwykle złożone obiekty matematyczne są fundamentem wielu dziedzin matematyki i znajdują zastosowanie w różnorodnych obszarach, od kryptografii po biologię. W tym artykule przyjrzymy się bliżej liczbom pierwszym, ich właściwościom, historii badań nad nimi oraz ich znaczeniu we współczesnym świecie.

Liczba pierwsza to liczba naturalna większa od 1, która ma dokładnie dwa dzielniki: 1 i samą siebie. Pierwszymi kilkoma liczbami pierwszymi są:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, …

Warto zauważyć, że:

Liczba 1 nie jest większą od 1 i ma tylko jeden dzielnik naturalny, więc nie jest liczbą pierwszą.

Najmniejszy różny od jedynki dzielnik naturalny liczby naturalnej, większej od jedności, jest liczbą pierwszą.

Liczba 2 jest jedyną parzystą liczbą pierwszą, więc wszystkie liczby pierwsze większe od 2 są nieparzyste.

Liczby pierwsze ≥5 (większe bądź równe 5) mają zawsze postać 6n±1 (6n-1 oraz 6n+1).

50% liczb w ciągu Fibonacciego to liczby mające postać 6n±1, czyli to liczby pierwsze i przypierwsze.

Liczby które są iloczynem bądź kwadratem dwóch liczb pierwszych ≥5 (większych bądź równych 5) to liczby przypierwsze, mają zawsze postać 6n±1. Odejmując ze zbioru liczb 6n±1 liczby będące iloczynami i kwadratami liczb ze zbioru 6n±1 otrzymamy wszystkie liczby pierwsze ≥5 (większe bądź równe 5) bez jakiejkolwiek faktoryzacji.

Liczby mające więcej niż dwa dzielniki to liczby złożone, np. liczba 4 ma już trzy dzielniki; są nimi 1, 2 oraz 4.

Nie ma największej liczby pierwszej – istnieje nieskończenie wiele liczb pierwszych. Euklides wykorzystując dowód przez sprzeczność, pokazał, że zbiór liczb pierwszych jest nieskończony. Dodatkowo Euklides w swoim dziele Elementy przedstawił pierwsze dowody na to, że liczby pierwsze są „fundamentalnymi składnikami” liczb naturalnych, czyli że każda liczba naturalna ≥4, nie będąca liczbą pierwszą, może być rozłożona na iloczyn liczb pierwszych. Na przykład: 4=2×2, 6=2×3, 8=2x2x2, 9=3×3 .

Największa znana liczba pierwsza (stan na 2023 rok) to 2^82,589,933^-1, która ma 24,862,048 cyfr. Największą znaną liczbą pierwszą, która nie jest liczbą Mersenne’a, jest: 10,223 ∙ 2^31172165 + 1, która została odkryta w roku 2016, a jej zapis dziesiętny liczy ponad 9 milionów cyfr.

Liczby pierwsze mają różne klasy i rodzaje, na przykład:

Liczby Bliźniacze: Dwie liczby pierwsze, których różnica wynosi 2, na przykład (3, 5), (11, 13). Pytanie, czy istnieje nieskończoność tych liczb, pozostaje nierozstrzygnięte.
Liczby Czworacze: Cztery liczby pierwsze, które są w postaci (p, p+2, p+6, p+8), np. (5, 7, 11, 13).
Liczby Mersenne’a: Liczby w postaci ( M(n) = 2^n – 1 ) są liczbami pierwszymi. Przykładami są 3, 7, 31, 127. Wiele z największych znanych liczb pierwszych to liczby Mersenne’a.
Liczby Germain: Liczby pierwsze p, dla których ( 2p + 1 ) również jest liczbą pierwszą, np. 2, 3, 5.

Historyczne momenty dotyczące liczb pierwszych

III wiek p.n.e. – Sito Eratostenesa, metoda znajdowania liczb pierwszych.
1640 – Pierre de Fermat formułuje Małe Twierdzenie Fermata.
1859 – Bernhard Riemann publikuje pracę o rozkładzie liczb pierwszych.
1896 – Jacques Hadamard i Charles Jean de la Vallée-Poussin niezależnie udowadniają twierdzenie o liczbach pierwszych.
2018 odkrycie wzoru na liczby pierwsze, odkrycie liczb przypierwszych.

Metody wyznaczania liczb pierwszych

Jedną z najbardziej znanych metod wyznaczania liczb pierwszych w danym przedziale jest sito Eratostenesa. Algorytm ten polega na tym, że:

Tworzy się listę liczb naturalnych od 2 do N.
Oznacza się pierwszą liczbę (2) i wykreśla jej wszystkie wielokrotności.
Powtarza się te kroki, aż do osiągnięcia końca listy.

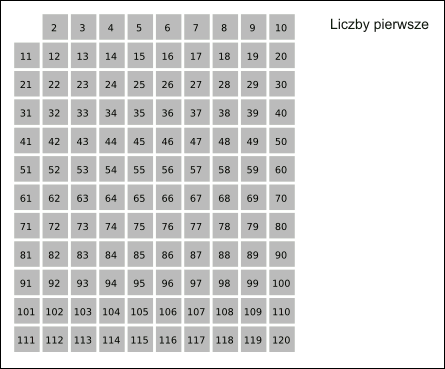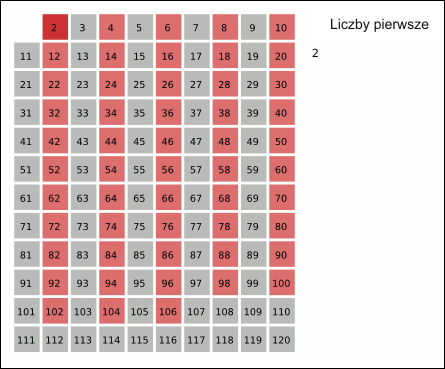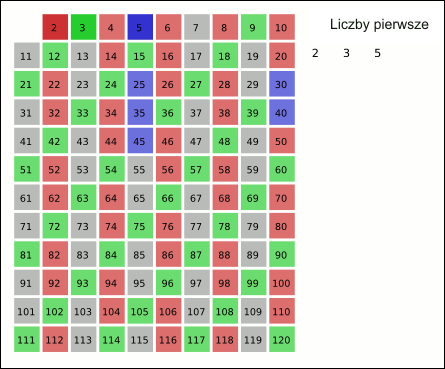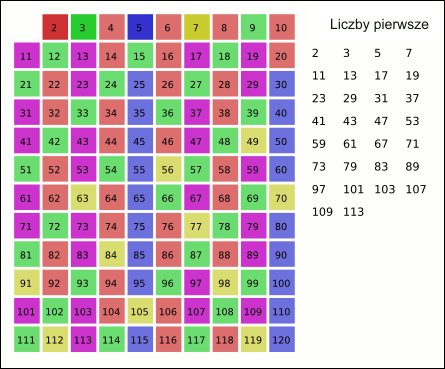
Animation_Sieb_des_Eratosthenes.gif: Saperaudderivative work: Bartek444, CC BY-SA 3.0 http://creativecommons.org/licenses/by-sa/3.0/, via Wikimedia Commons

Istnieje wiele innych metod znajdowania liczb pierwszych. Oto kilka z nich:

Test pierwszości – algorytmy sprawdzające, czy dana liczba jest pierwsza jest test pierwszości Solovaya-Strassena.
Test Millera-Rabina – probabilistyczny test pierwszości, często używany w praktyce w przypadku bardzo dużych liczb.
Metoda AKS – deterministyczny algorytm testowania pierwszości w czasie wielomianowym.
Jednak najbardziej optymalną i bezbłędną metodą znajdowania liczb pierwszych, pozbawioną faktoryzacji jest zastosowanie poniższego wzoru:

{(2), (3), (5), (6m+1), (6n-1) | m > 0, m mod 10 ≠ 4, m mod 10 ≠ 9, n > 0, n mod 10 ≠ 1, n mod 10 ≠ 6} \ {(6m+1)*(6n-1), (6m+1)*(6m+1), (6n-1)*(6n-1) | m > 0, m mod 10 ≠ 4, m mod 10 ≠ 9, n > 0 , n mod 10 ≠ 1, n mod 10 ≠ 6}

Więcej informacji o tym wzorze w zakładce KOD LICZB PIERWSZYCH.

Rozkład i występowanie liczb pierwszych

Jednym z najważniejszych zagadnień związanych z liczbami pierwszymi jest ich rozkład. Mimo że liczby pierwsze wydają się pojawiać dość nieregularnie, istnieją pewne prawidłowości w ich rozkładzie.

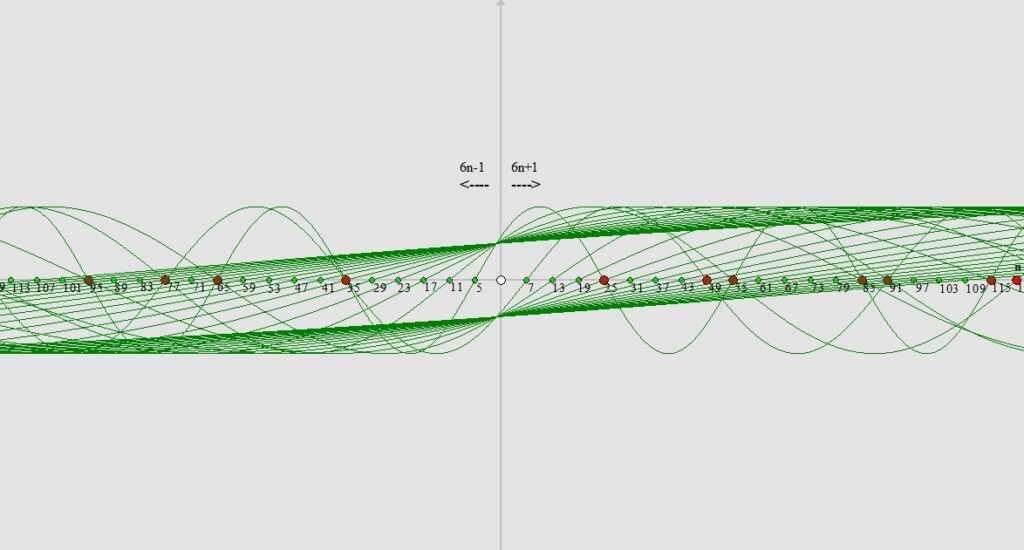
Twierdzenie o liczbach pierwszych mówi, że gęstość liczb pierwszych maleje logarytmicznie wraz ze wzrostem rozważanych liczb. Dokładniej, liczba liczb pierwszych nie przekraczających n jest asymptotycznie równa n/ln(n). Leonhard Euler udowodnił, że szereg odwrotności wszystkich liczb pierwszych jest rozbieżny. To sugeruje, że liczby pierwsze są rozłożone w taki sposób, że nie mogą być zbyt rzadko rozmieszczone na osi liczbowej, co prowadzi do wniosku o istnieniu nieskończonej liczby liczb pierwszych.
Rozmieszczenie liczb pierwszych na osi liczbowej jest interesującym tematem badań matematycznych. Odkrycia takie jak spirala Ulama sugerowały pewne statystyczne prawidłowości, ale istnieje uporządkowany i jednolity schemat występowania liczb pierwszych.

Więcej informacji w zakładce LICZBY PRZYPIERWSZE.

Problemy dotyczące liczb pierwszych

Mimo wielu lat badań, wciąż istnieje wiele nierozwiązanych problemów związanych z liczbami pierwszymi. Oto niektóre z nich:

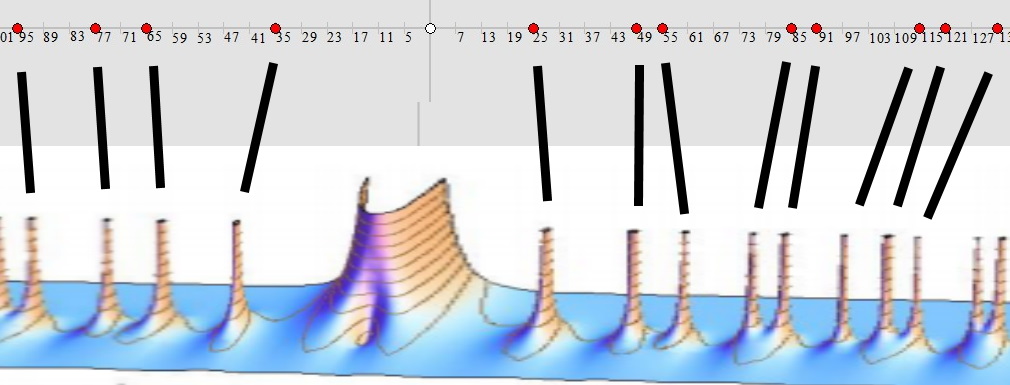
Hipoteza Riemanna – dotyczy rozkładu liczb pierwszych i jest uważana za jeden z najważniejszych nierozwiązanych problemów matematyki. Jednak występowanie miejsc zerowych funkcji Riemanna oraz rozkład poziomów energetycznych jąder atomów ciężkich jest mocno uzależnione także od liczb przypierwszych, a nie jak powszechnie się sądzi tylko od liczb pierwszych.
Hipoteza liczb pierwszych bliźniaczych – czy istnieje nieskończenie wiele par liczb pierwszych różniących się o 2?
Hipoteza Goldbacha – czy każda parzysta liczba większa od 2 jest sumą dwóch liczb pierwszych?
Problem istnienia nieskończenie wielu liczb pierwszych Mersenne’a.
Liczby pierwsze w ciągu Fibonacciego.
Obecność liczby pierwszej w przedziale pomiędzy ( n^2 ) a ( (n+1)^2 ).

Zastosowanie liczb pierwszych

Liczby pierwsze mają wiele praktycznych zastosowań, zwłaszcza w dziedzinie kryptografii i bezpieczeństwa cyfrowego. Oto niektóre z nich:

Kryptografia asymetryczna – systemy RSA i ElGamal opierają się na trudności faktoryzacji dużych liczb na czynniki pierwsze.
Generowanie kluczy w kryptografii – duże liczby pierwsze są używane do generowania bezpiecznych kluczy.
Kody korekcyjne – niektóre kody korekcyjne wykorzystują właściwości liczb pierwszych.
Generatory liczb pseudolosowych – liczby pierwsze są wykorzystywane w niektórych algorytmach generowania liczb pseudolosowych.

Ciekawostki o liczbach pierwszych

Liczby pierwsze Mersenne’a to liczby pierwsze postaci 2^p – 1, gdzie p jest liczbą pierwszą.
Liczby pierwsze Fermata to liczby postaci 2^(2^n) + 1. Pierwsze pięć to liczby pierwsze, ale nie wiadomo, czy istnieją inne.
Istnieją liczby pierwsze, które pozostają pierwsze po usunięciu dowolnej liczby cyfr z lewej strony – nazywamy je liczbami pierwszymi przycięcia z lewej strony, np. 23 (3), 317 (17) (7), 3797 (797) (97) (7).

Liczby pierwsze do 100, 1000, 10000, 100000 oraz pierwsze 10000 liczb pierwszych znajdziemy tutaj.

Liczby pierwsze, mimo swojej pozornej prostoty, kryją w sobie wiele tajemnic i nadal stanowią przedmiot intensywnych badań matematycznych. Ich właściwości i zastosowania sprawiają, że pozostają one jednym z najbardziej fascynujących obszarów matematyki. Jednak świat nauki powinien lepiej przyjrzeć się również iloczynom i kwadratom liczb pierwszych i uwzględnić liczby przypierwsze jako liczby równie ważne jak liczby pierwsze.

Ten artykuł jest dostępny także w języku angielskim, kliknij tutaj.